Math416 Lecture 11

Continue on integration over complex plane

Continue on last example

Last lecture we have:Let $R$ be a rectangular start from the $-a$ to $a$, $a+ib$ to $-a+ib$, $\int_{R} e^{-z^2}dz=0$, however, the integral consists of four parts:

Path 1: $-a\to a$

$\int_{I_1}e^{-z^2}dz=\int_{-a}^{a}e^{-z^2}dz=\int_{-a}^{a}e^{-x^2}dx$

Path 2: $a+ib\to -a+ib$

$\int_{I_2}e^{-z^2}dz=\int_{a+ib}^{-a+ib}e^{-z^2}dz=\int_{0}^{b}e^{-(a+iy)^2}dy$

Path 3: $-a+ib\to -a-ib$

$-\int_{I_3}e^{-z^2}dz=-\int_{-a+ib}^{-a-ib}e^{-z^2}dz=-\int_{a}^{-a}e^{-(x-ib)^2}dx$

Path 4: $-a-ib\to a-ib$

$-\int_{I_4}e^{-z^2}dz=-\int_{-a-ib}^{a-ib}e^{-z^2}dz=-\int_{b}^{0}e^{-(-a+iy)^2}dy$

The reverse of a curve 6.9

If $\gamma:[a,b]\to\mathbb{C}$ is a curve, then the rever of $\gamma$ is the curve $-\gamma:[-b,-a]\to\mathbb{C}$ defined by $(-\gamma)(t)=\gamma(a+b-t)$. It is the curve one obtains from $\gamma$ by traversing it in the opposite direction.

• If $\gamma$ is piecewise in $C^1$, then $-\gamma$ is piecewise in $C^1$.
• $\int_{-\gamma}f(z)dz=-\int_{\gamma}f(z)dz$ for any function $f$ that is continuous on $\gamma([a,b])$.

If we keep $b$ fixed, and let $a\to\infty$, then

Definition 6.10 (Estimate of the integral)

Let $\gamma:[a,b]\to\mathbb{C}$ be a piecewise $C^1$ curve, and let $f:[a,b]\to\mathbb{C}$ be a continuous complex-valued function. Let $M$ be the maximum of $|f|$ on $\gamma([a,b])$. ($M=\max\{|f(t)|:t\in[a,b]\}$)

Then

$\left|\int_{\gamma}f(z)dz\right|\leq L(\gamma)M$

Continue on previous example, we have:

Since,

Since $\sin 2bx$ is odd, and $\cos 2bx$ is even, we have

Proof for the last step:

Proof:

Let $J=\int_{-\infty}^{\infty}e^{-x^2}dx$

Then

$J^2=\int_{-\infty}^{\infty}e^{-x^2}dx\int_{-\infty}^{\infty}e^{-y^2}dy=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-(x^2+y^2)}dxdy$

We can evaluate the integral on the right-hand side by converting to polar coordinates. $x=r\cos\theta$, $y=r\sin\theta,dxdy=rdrd\theta$

QED

Chapter 7 Cauchy’s theorem

Cauchy’s theorem (Fundamental theorem of complex function theory)

Let $\gamma$ be a closed curve in $\mathbb{C}$ and let $u$ be an open set containing $\gamma^*$. Let $f$ be a holomorphic function on $u$. Then

Note: What “containing $\gamma^*$” means? (Rabbit hole for topologists)

Lemma 7.1 (Goursat’s lemma)

Cauchy’s theorem is true if $\gamma$ is a triangle.

Proof:

We plan to keep shrinking the triangle until $f(z+h)=f(z)+hf'(z)+\epsilon(h)$ where $\epsilon(h)$ is a function of $h$ that goes to $0$ as $h\to 0$.

Let’s start with a triangle $T$ with vertices $z_1,z_2,z_3$.

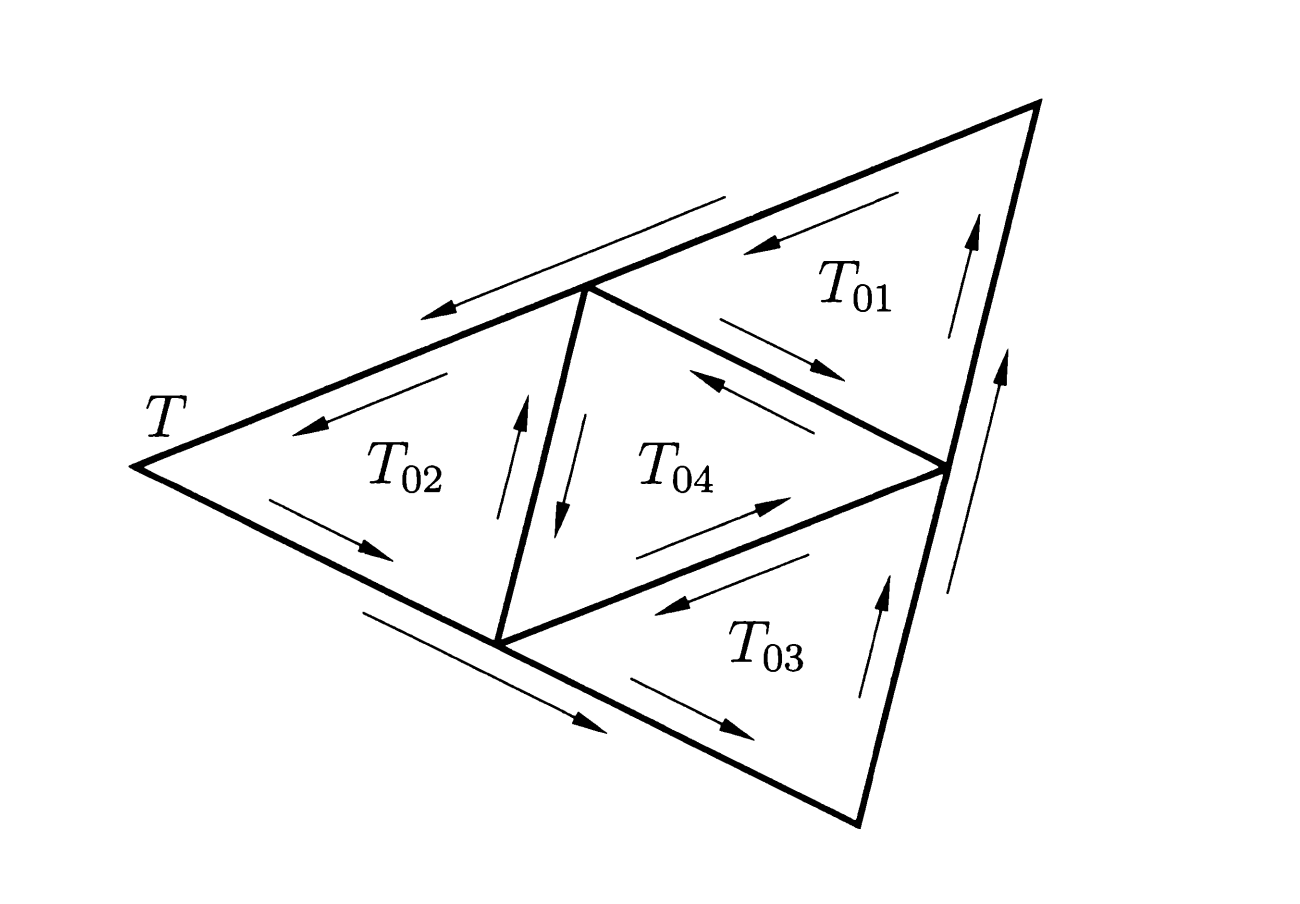
We divide $T$ into four smaller triangles by drawing lines from the midpoints of the sides to the opposite vertices.

Let $R_1,\ldots,R_4$ be the four smaller triangles.

For one $R_j$, $\left|\int_{R_j}f(z)dz\right|\geq\frac{1}{4}|I|$, we choose it then call it $T_1$.

There exists $T_1$ such that $\left|\int_{T_1}f(z)dz\right|\geq\frac{1}{4}|I|$.

Since $L(T_1)=\frac{1}{2}L(T)$, we iterate after $n$ steps, get a triangle $T_n$ such that $L(T_n)=\frac{L(T)}{2^n}$ and $\left|\int_{T_n}f(z)dz\right|\geq\frac{1}{4^n}|I|$.

Since $K_n=T_n\cup \text{interior}(T_n)$ is compact, we can find $K_n+1\subset K_n$ and $diam(K_n+1)<\frac{1}{2}diam(K_n)$. $diam(K_n)\to 0$ as $n\to\infty$. (Using completeness theorem)

Since $f$ is holomorphic on $u$, $\lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}=f'(z_0)$ exists.

So $f(z)=f(z_0)+f'(z_0)(z-z_0)+R(z)$, we have

since $f(z_0)dz+\int_{T_n}f'(z_0)(z-z_0)$ is in form of Cauchy integral formula, we have

Let $e_n=\max\{\frac{R(z)}{z-z_0}:z_0\in T_n\}$

Since $diam(K_n)\to 0$ as $n\to\infty$, we have $e_n\to 0$ as $n\to\infty$.

So

Since $e_n\to 0$ as $n\to\infty$, we have $I\to 0$ as $n\to\infty$.

So

QED