Math 416 Midterm 1 Review

So everything we have learned so far is to extend the real line to the complex plane.

Chapter 0 Calculus on Real values

Differentiation

Let $f,g$ be function on real line and $c$ be a real number.

\frac{d}{dx}(f+g)=f'+g'

\frac{d}{dx}(cf)=cf'

\frac{d}{dx}(fg)=f'g+fg'

\frac{d}{dx}(f/g)=(f'g-fg')/g^2

\frac{d}{dx}(f\circ g)=(f'\circ g)\frac{d}{dx}g

\frac{d}{dx}x^n=nx^{n-1}

\frac{d}{dx}e^x=e^x

\frac{d}{dx}\ln x=\frac{1}{x}

\frac{d}{dx}\sin x=\cos x

\frac{d}{dx}\cos x=-\sin x

\frac{d}{dx}\tan x=\sec^2 x

\frac{d}{dx}\sec x=\sec x\tan x

\frac{d}{dx}\csc x=-\csc x\cot x

\frac{d}{dx}\sinh x=\cosh x

\frac{d}{dx}\cosh x=\sinh x

\frac{d}{dx}\tanh x=\operatorname{sech}^2 x

\frac{d}{dx}\operatorname{sech} x=-\operatorname{sech}x\tanh x

\frac{d}{dx}\operatorname{csch} x=-\operatorname{csch}x\coth x

\frac{d}{dx}\coth x=-\operatorname{csch}^2 x

\frac{d}{dx}\arcsin x=\frac{1}{\sqrt{1-x^2}}

\frac{d}{dx}\arccos x=-\frac{1}{\sqrt{1-x^2}}

\frac{d}{dx}\arctan x=\frac{1}{1+x^2}

\frac{d}{dx}\operatorname{arccot} x=-\frac{1}{1+x^2}

\frac{d}{dx}\operatorname{arcsec} x=\frac{1}{x\sqrt{x^2-1}}

\frac{d}{dx}\operatorname{arccsc} x=-\frac{1}{x\sqrt{x^2-1}}

Integration

Let $f,g$ be function on real line and $c$ be a real number.

\int (f+g)dx=\int fdx+\int gdx

\int cfdx=c\int fdx

\int e^x dx=e^x

\int \ln x dx=x\ln x-x

\int \frac{1}{x} dx=\ln|x|

\int \sin x dx=-\cos x

\int \cos x dx=\sin x

\int \tan x dx=-\ln|\cos x|

\int \cot x dx=\ln|\sin x|

\int \sec x dx=\ln|\sec x+\tan x|

\int \csc x dx=\ln|\csc x-\cot x|

\int \sinh x dx=\cosh x

\int \cosh x dx=\sinh x

\int \tanh x dx=\ln|\cosh x|

\int \coth x dx=\ln|\sinh x|

\int \operatorname{sech} x dx=2\arctan(\tanh(x/2))

\int \operatorname{csch} x dx=\ln|\coth x-\operatorname{csch} x|

\int \operatorname{sech}^2 x dx=\tanh x

\int \operatorname{csch}^2 x dx=-\coth x

\int \frac{1}{1+x^2} dx=\arctan x

\int \frac{1}{x^2+1} dx=\arctan x

\int \frac{1}{x^2-1} dx=\frac{1}{2}\ln|\frac{x-1}{x+1}|

\int \frac{1}{x^2-a^2} dx=\frac{1}{2a}\ln|\frac{x-a}{x+a}|

\int \frac{1}{x^2+a^2} dx=\frac{1}{a}\arctan(\frac{x}{a})

\int \frac{1}{\sqrt{x^2-a^2}} dx=\ln|x+\sqrt{x^2-a^2}|

\int \frac{1}{\sqrt{x^2+a^2}} dx=\ln|x+\sqrt{x^2+a^2}|

Chapter 1 Complex Numbers

Definition of complex numbers

An ordered pair of real numbers $(x, y)$ can be represented as a complex number $z = x + yi$ , where $i$ is the imaginary unit.

With operations defined as:

(x_1 + y_1i) + (x_2 + y_2i) = (x_1 + x_2) + (y_1 + y_2)i

(x_1 + y_1i) \cdot (x_2 + y_2i) = (x_1x_2 - y_1y_2) + (x_1y_2 + x_2y_1)i

Modulus

The modulus of a complex number $z = x + yi$ is defined as

|z| = \sqrt{x^2 + y^2}=|z\overline{z}|

De Moivre’s Formula

Every complex number $z$ can be written as $z = r(\cos \theta + i \sin \theta)$ , where $r$ is the magnitude of $z$ and $\theta$ is the argument of $z$ .

z^n = r^n(\cos n\theta + i \sin n\theta)

The De Moivre’s formula is useful for finding the $n$ th roots of a complex number.

z^n = r^n(\cos n\theta + i \sin n\theta)

Roots of complex numbers

Using De Moivre’s formula, we can find the $n$ th roots of a complex number.

If $z=r(\cos \theta + i \sin \theta)$ , then the $n$ th roots of $z$ are given by:

z_k = r^{1/n}(\cos \frac{\theta + 2k\pi}{n} + i \sin \frac{\theta + 2k\pi}{n})

for $k = 0, 1, 2, \ldots, n-1$ .

Stereographic projection

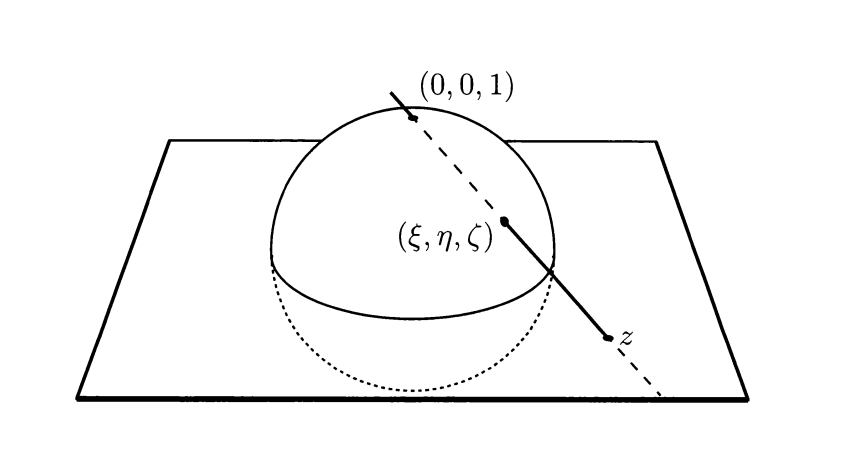
The stereographic projection is a map from the unit sphere $S^2$ to the complex plane $\mathbb{C}\setminus\{0\}$ .

The projection is given by:

z\mapsto \frac{(2Re(z), 2Im(z), |z|^2-1)}{|z|^2+1}

The inverse map is given by:

(\xi,\eta, \zeta)\mapsto \frac{\xi + i\eta}{1 - \zeta}

Chapter 2 Complex Differentiation

Definition of complex differentiation

Let the complex plane $\mathbb{C}$ be defined in an open subset $G$ of $\mathbb{C}$ . (Domain)

Then $f$ is said to be differentiable at $z_0\in G$ if the limit

\lim_{z\to z_0} \frac{f(z)-f(z_0)}{z-z_0}

exists.

The limit is called the derivative of $f$ at $z_0$ and is denoted by $f'(z_0)$ .

To prove that a function is differentiable, we can use the standard delta-epsilon definition of a limit.

\left|\frac{f(z)-f(z_0)}{z-z_0} - f'(z_0)\right| < \epsilon

whenever $0 < |z-z_0| < \delta$ .

With such definition, all the properties of real differentiation can be extended to complex differentiation.

Differentiation of complex functions

If $f$ is differentiable at $z_0$ , then $f$ is continuous at $z_0$ .
If $f,g$ are differentiable at $z_0$ , then $f+g, fg$ are differentiable at $z_0$ . $(f+g)'(z_0) = f'(z_0) + g'(z_0)$ $(fg)'(z_0) = f'(z_0)g(z_0) + f(z_0)g'(z_0)$
If $f,g$ are differentiable at $z_0$ and $g(z_0)\neq 0$ , then $f/g$ is differentiable at $z_0$ . $\left(\frac{f}{g}\right)'(z_0) = \frac{f'(z_0)g(z_0) - f(z_0)g'(z_0)}{g(z_0)^2}$
If $f$ is differentiable at $z_0$ and $g$ is differentiable at $f(z_0)$ , then $g\circ f$ is differentiable at $z_0$ . $(g\circ f)'(z_0) = g'(f(z_0))f'(z_0)$
If $f(z)=\sum_{k=0}^n c_k(z-z_0)^k$ , where $c_k\in\mathbb{C}$ , then $f$ is differentiable at $z_0$ and $f'(z_0)=\sum_{k=1}^n kc_k(z_0-z_0)^{k-1}$ . $f'(z_0) = c_1 + 2c_2(z_0-z_0) + 3c_3(z_0-z_0)^2 + \cdots + nc_n(z_0-z_0)^{n-1}$

Cauchy-Riemann Equations

Let the function defined on an open subset $G$ of $\mathbb{C}$ be $f(x,y)=u(x,y)+iv(x,y)$ , where $u,v$ are real-valued functions.

Then $f$ is differentiable at $z_0=x_0+y_0i$ if and only if the partial derivatives of $u$ and $v$ exist at $(x_0,y_0)$ and satisfy the Cauchy-Riemann equations:

\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}

On the polar form, the Cauchy-Riemann equations are

r\frac{\partial u}{\partial r} = \frac{\partial v}{\partial \theta}, \quad \frac{\partial u}{\partial \theta} = -r\frac{\partial v}{\partial r}

Holomorphic functions

A function $f$ is said to be holomorphic on an open subset $G$ of $\mathbb{C}$ if $f$ is differentiable at every point of $G$ .

Partial differential operators

\frac{\partial}{\partial z} = \frac{1}{2}\left(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}\right)

\frac{\partial}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial}{\partial x} + i\frac{\partial}{\partial y}\right)

This gives that

\frac{\partial f}{\partial z} = \frac{1}{2}\left(\frac{\partial f}{\partial x} - i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\right)

\frac{\partial f}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial f}{\partial x} + i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right)

If the function $f$ is holomorphic, then by the Cauchy-Riemann equations, we have

\frac{\partial f}{\partial \bar{z}} = 0

Conformal mappings

A holomorphic function $f$ is said to be conformal if it preserves the angles between the curves. More formally, if $f$ is holomorphic on an open subset $G$ of $\mathbb{C}$ and $z_0\in G$ , $\gamma_1, \gamma_2$ are two curves passing through $z_0$ ( $\gamma_1(t_1)=\gamma_2(t_2)=z_0$ ) and intersecting at an angle $\theta$ , then

\arg(f\circ\gamma_1)'(t_1) - \arg(f\circ\gamma_2)'(t_2) = \theta

In other words, the angle between the curves is preserved.

An immediate consequence is that

\arg(f\cdot \gamma_1)'(t_1) =\arg f'(z_0) + \arg \gamma_1'(t_1)\\ \arg(f\cdot \gamma_2)'(t_2) =\arg f'(z_0) + \arg \gamma_2'(t_2)

Harmonic functions

A real-valued function $u$ is said to be harmonic if it satisfies the Laplace equation:

\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0

Chapter 3 Linear Fractional Transformations

Definition of linear fractional transformations

A linear fractional transformation is a function of the form

\phi(z) = \frac{az+b}{cz+d}

where $a,b,c,d$ are complex numbers and $ad-bc\neq 0$ .

Properties of linear fractional transformations

Matrix form

A linear fractional transformation can be written as a matrix multiplication:

\phi(z) = \begin{bmatrix} a & b\\ c & d\\ \end{bmatrix} \begin{bmatrix} z\\ 1\\ \end{bmatrix}

Conformality

A linear fractional transformation is conformal.

\phi'(z) = \frac{ad-bc}{(cz+d)^2}

Three-fold transitivity

If $z_1,z_2,z_3$ are distinct points in the complex plane, then there exists a unique linear fractional transformation $\phi$ such that $\phi(z_1)=\infty$ , $\phi(z_2)=0$ , $\phi(z_3)=1$ .

The map is given by

\phi(z) =\begin{cases} \frac{(z-z_2)(z_1-z_3)}{(z-z_1)(z_2-z_3)} & \text{if } z_1,z_2,z_3 \text{ are all finite}\\ \frac{z-z_2}{z_3-z_2} & \text{if } z_1=\infty\\ \frac{z_3-z_1}{z-z_1} & \text{if } z_2=\infty\\ \frac{z-z_2}{z-z_1} & \text{if } z_3=\infty\\ \end{cases}

So if $z_1,z_2,z_3$ , $w_1,w_2,w_3$ are distinct points in the complex plane, then there exists a unique linear fractional transformation $\phi$ such that $\phi(z_i)=w_i$ for $i=1,2,3$ .

Factorization

Every linear fractional transformation can be written as a composition of homothetic mappings, translations, inversions, and multiplications.

If $\phi(z)=\frac{az+b}{cz+d}$ , then

\phi(z) = \frac{b-ad/c}{cz+d}+\frac{a}{c}

Clircle

A linear-fractional transformation maps circles and lines to circles and lines.

Chapter 4 Elementary Functions

Exponential function

The exponential function is defined as

e^z = \sum_{n=0}^\infty \frac{z^n}{n!}

Let $z=x+iy$ , then

\begin{aligned} e^z &= e^{x+iy}\\ &= e^x e^{iy}\\ &= e^x\sum_{n=0}^\infty \frac{(iy)^n}{n!}\\ &= e^x\sum_{n=0}^\infty \frac{(-1)^n y^{2n}}{(2n)!} + i \sum_{n=0}^\infty \frac{(-1)^n y^{2n+1}}{(2n+1)!}\\ &= e^x(\cos y + i\sin y)\\ \end{aligned}

So we can rewrite the polar form of a complex number as

z = r(\cos \theta + i\sin \theta) = re^{i\theta}

$e^x$ is holomorphic

Let $f(z)=e^z$ , then $u(x,y)=e^x\cos y$ , $v(x,y)=e^x\sin y$ .

\frac{\partial u}{\partial x} = e^x\cos y = \frac{\partial v}{\partial y}\\ \frac{\partial u}{\partial y} = -e^x\sin y = -\frac{\partial v}{\partial x}

Trigonometric functions

\sin z = \frac{e^{iz}-e^{-iz}}{2i}, \quad \cos z = \frac{e^{iz}+e^{-iz}}{2}, \quad \tan z = \frac{\sin z}{\cos z}

\sec z = \frac{1}{\cos z}, \quad \csc z = \frac{1}{\sin z}, \quad \cot z = \frac{1}{\tan z}

Hyperbolic functions

\sinh z = \frac{e^z-e^{-z}}{2}, \quad \cosh z = \frac{e^z+e^{-z}}{2}, \quad \tanh z = \frac{\sinh z}{\cosh z}

\operatorname{sech} z = \frac{1}{\cosh z}, \quad \operatorname{csch} z = \frac{1}{\sinh z}, \quad \operatorname{coth} z = \frac{1}{\tanh z}

Logarithmic function

The logarithmic function is defined as

\ln z=\{w\in\mathbb{C}: e^w=z\}

Properties of the logarithmic function

Let $z=x+iy$ , then

|e^z|=\sqrt{e^x(\cos y)^2+(\sin y)^2}=e^x

So we have

\log z = \ln |z| + i\arg z

Power function

For any two complex numbers $a,b$ , we can define the power function as

a^b = e^{b\log a}

Example:

$i^i=e^{i\ln i}=e^{i(\ln 1+i\frac{\pi}{2})}=e^{-\frac{\pi}{2}}$

$e^{i\pi}=-1$

Chapter 5 Power Series

Definition of power series

A power series is a series of the form

\sum_{n=0}^\infty a_n (z-z_0)^n

Properties of power series

Geometric series

\sum_{n=0}^\infty z^n = \frac{1}{1-z}, \quad |z|<1

Radius/Region of convergence

The radius of convergence of a power series is the largest number $R$ such that the series converges for all $z$ with $|z-z_0|<R$ .

The region of convergence of a power series is the set of all points $z$ such that the series converges.

Cauchy-Hadamard Theorem

The radius of convergence of a power series is given by

R=\frac{1}{\limsup_{n\to\infty} |a_n|^{1/n}}

Derivative of power series

The derivative of a power series is given by

f'(z)=\sum_{n=1}^\infty n a_n (z-z_0)^{n-1}

Cauchy Product (of power series)

Let $\sum_{n=0}^\infty a_n (z-z_0)^n$ and $\sum_{n=0}^\infty b_n (z-z_0)^n$ be two power series with radius of convergence $R_1$ and $R_2$ respectively.

Then the Cauchy product of the two series is given by

\sum_{n=0}^\infty c_n (z-z_0)^n

where

c_n = \sum_{k=0}^n a_k b_{n-k}

The radius of convergence of the Cauchy product is at least $\min(R_1,R_2)$ .

Chapter 6 Complex Integration

Definition of Riemann Integral for complex functions

The complex integral of a complex function $\phi$ on the closed subinterval $[a,b]$ of the real line is said to be piecewise continuous if there exists a partition $a=t_0<t_1<\cdots<t_n=b$ such that $\phi$ is continuous on each open interval $(t_{i-1},t_i)$ and has a finite limit at each discontinuity point of the closed interval $[a,b]$ .

If $\phi$ is piecewise continuous on $[a,b]$ , then the complex integral of $\phi$ on $[a,b]$ is defined as

\int_a^b \phi(t) dt = \int_a^b \operatorname{Re}\phi(t) dt + i\int_a^b \operatorname{Im}\phi(t) dt

Fundamental Theorem of Calculus

If $\phi$ is piecewise continuous on $[a,b]$ , then

\int_a^b \phi'(t) dt = \phi(b)-\phi(a)

Triangle inequality

\left|\int_a^b \phi(t) dt\right| \leq \int_a^b |\phi(t)| dt

Integral on curve

Let $\gamma$ be a piecewise smooth curve in the complex plane.

The integral of a complex function $f$ on $\gamma$ is defined as

\int_\gamma f(z) dz = \int_a^b f(\gamma(t))\gamma'(t) dt

Favorite estimate

Let $\gamma:[a,b]\to\mathbb{C}$ be a piecewise smooth curve, and let $f:[a,b]\to\mathbb{C}$ be a continuous complex-valued function. Let $M$ be a real number such that $|f(z)|\leq M$ for all $z\in\gamma$ . Then

\left|\int_\gamma f(z) dz\right| \leq M\ell(\gamma)

where $\ell(\gamma)$ is the length of the curve $\gamma$ .

Chapter 7 Cauchy’s Theorem

Cauchy’s Theorem

Let $\gamma$ be a closed curve in $\mathbb{C}$ and $U$ be a simply connected open subset of $\mathbb{C}$ containing $\gamma$ and its interior. Let $f$ be a holomorphic function on $U$ . Then

\int_\gamma f(z) dz = 0

Cauchy’s Formula for a Circle

Let $C$ be a counterclockwise oriented circle and let $f$ be holomorphic function defined in an open set containing $C$ and its interior. Then for any $z$ in the interior of $C$ ,

f(z)=\frac{1}{2\pi i}\int_C \frac{f(\zeta)}{\zeta-z} d\zeta

Mean Value Property

Let the function $f$ be holomorphic on a disk $|z-z_0|<R$ . Then for any $0<r<R$ , let $C_r$ denote the circle with center $z_0$ and radius $r$ . Then

f(z_0)=\frac{1}{2\pi}\int_0^{2\pi} f(z_0+re^{i\theta}) d\theta

The value of the function at the center of the disk is the average of the values of the function on the boundary of the disk.

Cauchy Integrals

Let $\gamma$ be a piecewise smooth curve in $\mathbb{C}$ and let $\phi$ be a continuous complex-valued function on $\gamma$ . Then the Cauchy integral of $\phi$ on $\gamma$ is the function $f$ defined in $C\setminus\gamma$ by

f(z)=\int_\gamma \frac{\phi(\zeta)}{\zeta-z} d\zeta

Cauchy Integral Formula for circle $C_r$ :

f(z)=\frac{1}{2\pi i}\int_{C_r} \frac{f(\zeta)}{\zeta-z} d\zeta

Example:

Evaluate $\int_{|z|=2} \frac{z}{z-1} dz$

Note that if we let $f(\zeta)=\zeta$ and $z=1$ is inside the circle, then we can use Cauchy Integral Formula for circle $C_r$ to evaluate the integral.

So we have

$\int_{|z|=2} \frac{z}{z-1} dz = 2\pi i f(1) = 2\pi i$

General Cauchy Integral Formula for circle $C_r$ :

f^{(n)}(z)=\frac{n!}{2\pi i}\int_{C_r} \frac{f(\zeta)}{(\zeta-z)^{n+1}} d\zeta

Example:

Evaluate $\int_{C}\frac{\sin z}{z^{38}}dz$

Note that if we let $f(\zeta)=\sin \zeta$ and $z=0$ is inside the circle, then we can use General Cauchy Integral Formula for circle $C_r$ to evaluate the integral.

So we have

$\int_{C}\frac{\sin z}{z^{38}}dz = \frac{2\pi i}{37!} f^{(37)}(0) = \frac{2\pi i}{37!} \sin ^{(37)}(0)$

Note that $\sin ^{(n)}(0)=\begin{cases} 0,& n\equiv 0 \pmod{4}\\ 1,& n\equiv 1 \pmod{4}\\ 0,& n\equiv 2 \pmod{4}\\ -1,& n\equiv 3 \pmod{4} \end{cases}$

So we have

$\int_{C}\frac{\sin z}{z^{38}}dz = \frac{2\pi i}{37!} \sin ^{(37)}(0) = \frac{2\pi i}{37!} \cdot 1 = \frac{2\pi i}{37!}$

Cauchy integral is a easier way to evaluate the integral.

Liouville’s Theorem

If a function $f$ is entire (holomorphic on $\mathbb{C}$ ) and bounded, then $f$ is constant.

Finding power series of holomorphic functions

If $f$ is holomorphic on a disk $|z-z_0|<R$ , then $f$ can be represented as a power series on the disk.

where $a_n=\frac{f^{(n)}(z_0)}{n!}$

Example:

If $q(z)=(z-1)(z-2)(z-3)$ , find the power series of $q(z)$ centered at $z=0$ .

Note that $q(z)$ is holomorphic on $\mathbb{C}$ and $q(z)=0$ at $z=1,2,3$ .

So we can use the power series of $q(z)$ centered at $z=1$ .

To solve this, we can simply expand $q(z)=(z-1)(z-2)(z-3)$ and get $q(z)=z^3-6z^2+11z-6$ .

So we have $a_0=q(1)=-6$ , $a_1=q'(1)=3z^2-12z+11=11$ , $a_2=\frac{q''(1)}{2!}=\frac{6z-12}{2}=-3$ , $a_3=\frac{q'''(1)}{3!}=\frac{6}{6}=1$ .

So the power series of $q(z)$ centered at $z=1$ is

$q(z)=-6+11(z-1)-3(z-1)^2+(z-1)^3$

Fundamental Theorem of Algebra

Every non-constant polynomial with complex coefficients has a root in $\mathbb{C}$ .

Can be factored into linear factors:

p(z)=a_n(z-z_1)(z-z_2)\cdots(z-z_n)

We can treat holomorphic functions as polynomials.

$f$ has zero of order $m$ at $z_0$ if and only if $f(z)=(z-z_0)^m g(z)$ for some holomorphic $g(z)$ and $g(z_0)\neq 0$ .

Zeros of holomorphic functions

If $f$ is holomorphic on a disk $|z-z_0|<R$ and $f$ has a zero of order $m$ at $z_0$ , then $f(z_0)=0$ , $f'(z_0)=0$ , $f''(z_0)=0$ , $\cdots$ , $f^{(m-1)}(z_0)=0$ and $f^{(m)}(z_0)\neq 0$ .

And there exists a holomorphic function $g$ on the disk such that $f(z)=(z-z_0)^m g(z)$ and $g(z_0)\neq 0$ .

Example:

Find zeros of $f(z)=\cos(z\frac{\pi}{2})$

Note that $f(z)=0$ if and only if $z\frac{\pi}{2}=(2k+1)\frac{\pi}{2}$ for some integer $k$ .

So the zeros of $f(z)$ are $z=(2k+1)$ for some integer $k$ .

The order of the zero is $1$ since $f'(z)=-\frac{\pi}{2}\sin(z\frac{\pi}{2})$ and $f'(z)\neq 0$ for all $z=(2k+1)$ .

If $f$ vanishes to infinite order at $z_0$ (that is, $f(z_0)=f'(z_0)=f''(z_0)=\cdots=0$ ), then $f(z)\equiv 0$ on the connected open set $U$ containing $z_0$ .

Identity Theorem

If $f$ and $g$ are holomorphic on a connected open set $U\subset\mathbb{C}$ and $f(z)=g(z)$ for all $z$ in a subset of $U$ that has a limit point in $U$ , then $f(z)=g(z)$ for all $z\in U$ .

Key: consider $h(z)=f(z)-g(z)$ , prove $h(z)\equiv 0$ on $U$ by applying the zero of holomorphic function.

Weierstrass Theorem

Limit of a sequence of holomorphic functions is holomorphic.

Let $f_n$ be a sequence of holomorphic functions on a domain $D\subset\mathbb{C}$ that converges uniformly to $f$ on every compact subset of $D$ . Then $f$ is holomorphic on $D$ .

Maximum Modulus Principle

If $f$ is a non-constant holomorphic function on a domain $D\subset\mathbb{C}$ , then $|f|$ does not attain a maximum value in $D$ .

Corollary: Minimum Modulus Principle

If $f$ is a non-constant holomorphic function on a domain $D\subset\mathbb{C}$ , then $\frac{1}{f}$ does not attain a minimum value in $D$ .

Schwarz Lemma

If $f$ is a holomorphic function on the unit disk $|z|<1$ and $|f(z)|\leq |z|$ , then $|f'(0)|\leq 1$ .