Math401 Topic 3: Separable Hilbert spaces

Infinite-dimensional Hilbert spaces

Recall from Topic 1.

$L^2$ space

Let $\lambda$ be a measure on $\mathbb{R}$, or any other field you are interested in.

A function is square integrable if

$L^2$ space and general Hilbert spaces

Definition of $L^2(\mathbb{R},\lambda)$

The space $L^2(\mathbb{R},\lambda)$ is the space of all square integrable, measurable functions on $\mathbb{R}$ with respect to the measure $\lambda$ (The Lebesgue measure).

The Hermitian inner product is defined by

The norm is defined by

The space $L^2(\mathbb{R},\lambda)$ is complete.

[Proof ignored here]

Recall the definition of complete metric space .

The inner product space $L^2(\mathbb{R},\lambda)$ is complete.

Note that by some general result in point-set topology, a normed vector space can always be enlarged so as to become complete. This process is called completion of the normed space.

Some exercise is showing some hints for this result:

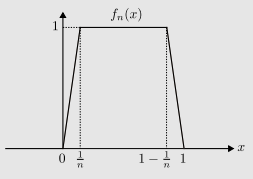
Show that the subspace of $L^2(\mathbb{R},\lambda)$ consisting of square integrable continuous functions is not closed.

Suggestion: consider the sequence of continuous functions $f_1(x), f_2(x),\cdots$, where $f_n(x)$ is defined by the following graph:

Show that $f_n$ converges in the $L^2$ norm to a function $f\in L^2(\mathbb{R},\lambda)$ but the limit function $f$ is not continuous. Draw the graph of $f_n$ to make this clear.

Definition of general Hilbert space

A Hilbert space is a complete inner product vector space.

General Pythagorean theorem

Let $u_1,u_2,\cdots,u_N$ be an orthonormal set in an inner product space $\mathscr{V}$ (may not be complete). Then for all $v\in \mathscr{V}$,

[Proof ignored here]

Bessel’s inequality

Let $u_1,u_2,\cdots,u_N$ be an orthonormal set in an inner product space $\mathscr{V}$ (may not be complete). Then for all $v\in \mathscr{V}$,

Immediate from the general Pythagorean theorem.

Orthonormal bases

An orthonormal subset $S$ of a Hilbert space $\mathscr{H}$ is a set all of whose elements have norm 1 and are mutually orthogonal. ($\forall u,v\in S, \langle u,v\rangle=0$)

Definition of orthonormal basis

An orthonormal subset of $S$ of a Hilbert space $\mathscr{H}$ is an orthonormal basis of $\mathscr{H}$ if there are no other orthonormal subsets of $\mathscr{H}$ that contain $S$ as a proper subset.

Theorem of existence of orthonormal basis

Every separable Hilbert space has an orthonormal basis.

[Proof ignored here]

Theorem of Fourier series

Let $\mathscr{H}$ be a separable Hilbert space with an orthonormal basis $\{e_n\}$. Then for any $f\in \mathscr{H}$,

The series converges to some $g\in \mathscr{H}$.

[Proof ignored here]

Fourier series in $L^2([0,2\pi],\lambda)$

Let $f\in L^2([0,2\pi],\lambda)$.

where $c_n=\frac{1}{2\pi}\int_0^{2\pi} f(x)e^{-inx} dx$.

The series converges to some $f\in L^2([0,2\pi],\lambda)$ as $N\to \infty$.

This is the Fourier series of $f$.

Hermite polynomials

The subspace spanned by polynomials is dense in $L^2(\mathbb{R},\lambda)$.

An orthonormal basis of $L^2(\mathbb{R},\lambda)$ can be obtained by the Gram-Schmidt process on $\{1,x,x^2,\cdots\}$.

The polynomials are called the Hermite polynomials.

Isomorphism and $\ell_2$ space

Definition of isomorphic Hilbert spaces

Let $\mathscr{H}_1$ and $\mathscr{H}_2$ be two Hilbert spaces.

$\mathscr{H}_1$ and $\mathscr{H}_2$ are isomorphic if there exists a surjective linear map $U:\mathscr{H}_1\to \mathscr{H}_2$ that is bijective and preserves the inner product.

for all $f,g\in \mathscr{H}_1$.

When $\mathscr{H}_1=\mathscr{H}_2$, the map $U$ is called unitary.

$\ell_2$ space

The space $\ell_2$ is the space of all square summable sequences.

An example of element in $\ell_2$ is $(1,0,0,\cdots)$.

With inner product

It is a Hilbert space (every Cauchy sequence in $\ell_2$ converges to some element in $\ell_2$).

Bounded operators and continuity

Let $T:\mathscr{V}\to \mathscr{W}$ be a linear map between two vector spaces $\mathscr{V}$ and $\mathscr{W}$.

We define the norm of $\|\cdot\|$ on $\mathscr{V}$ and $\mathscr{W}$.

Then $T$ is continuous if for all $u\in \mathscr{V}$, if $u_n\to u$ in $\mathscr{V}$, then $T(u_n)\to T(u)$ in $\mathscr{W}$.

Using the delta-epsilon language, we can say that $T$ is continuous if for all $\epsilon>0$, there exists a $\delta>0$ such that if $\|u-v\|<\delta$, then $\|T(u)-T(v)\|<\epsilon$.

Definition of bounded operator

A linear map $T:\mathscr{V}\to \mathscr{W}$ is bounded if

Theorem of continuity and boundedness

A linear map $T:\mathscr{V}\to \mathscr{W}$ is continuous if and only if it is bounded.

[Proof ignored here]

Definition of bounded Hilbert space

The set of all bounded linear operators in $\mathscr{V}$ is denoted by $\mathscr{B}(\mathscr{V})$.

Direct sum of Hilbert spaces

Suppose $\mathscr{H}_1$ and $\mathscr{H}_2$ are two Hilbert spaces.

The direct sum of $\mathscr{H}_1$ and $\mathscr{H}_2$ is the Hilbert space $\mathscr{H}_1\oplus \mathscr{H}_2$ with the inner product

Such space is denoted by $\mathscr{H}_1\oplus \mathscr{H}_2$.

A countable direct sum of Hilbert spaces can be defined similarly, as long as it is bounded.

That is, $\{u_n:n=1,2,\cdots\}$ is a sequence of elements in $\mathscr{H}_n$, and $\sum_{n=1}^\infty \|u_n\|^2<\infty$.

The inner product in such countable direct sum is defined by

Such space is denoted by $\mathscr{H}=\bigoplus_{n=1}^\infty \mathscr{H}_n$.

Closed subspaces of Hilbert spaces

Definition of closed subspace

A subspace $\mathscr{M}$ of a Hilbert space $\mathscr{H}$ is closed if every convergent sequence in $\mathscr{M}$ converges to some element in $\mathscr{M}$.

Definition of pairwise orthogonal subspaces

Two subspaces $\mathscr{M}_1$ and $\mathscr{M}_2$ of a Hilbert space $\mathscr{H}$ are pairwise orthogonal if $\langle u,v\rangle=0$ for all $u\in \mathscr{M}_1$ and $v\in \mathscr{M}_2$.

Orthogonal projections

Definition of orthogonal complement

The orthogonal complement of a subspace $\mathscr{M}$ of a Hilbert space $\mathscr{H}$ is the set of all elements in $\mathscr{H}$ that are orthogonal to every element in $\mathscr{M}$.

It is denoted by $\mathscr{M}^\perp=\{u\in \mathscr{H}: \langle u,v\rangle=0,\forall v\in \mathscr{M}\}$.

Projection theorem

Let $\mathscr{H}$ be a Hilbert space and $\mathscr{M}$ be a closed subspace of $\mathscr{H}$. Then for any $v\in \mathscr{H}$ can be uniquely decomposed as $v=u+w$ where $u\in \mathscr{M}$ and $w\in \mathscr{M}^\perp$.

[Proof ignored here]

Dual Hilbert spaces

Norm of linear functionals

Let $\mathscr{H}$ be a Hilbert space.

The norm of a linear functional $f\in \mathscr{H}^*$ is defined by

Definition of dual Hilbert space

The dual Hilbert space of $\mathscr{H}$ is the space of all bounded linear functionals on $\mathscr{H}$.

It is denoted by $\mathscr{H}^*$.

You can exchange the $\mathbb{C}$ with any other field you are interested in.

The Riesz lemma

For each $f\in \mathscr{H}^*$, there exists a unique $v_f\in \mathscr{H}$ such that $f(u)=\langle u,v_f\rangle$ for all $u\in \mathscr{H}$. And $\|f\|=\|v_f\|$.

[Proof ignored here]

Definition of bounded sesqilinear form

A bounded sesqilinear form on $\mathscr{H}$ is a function $B: \mathscr{H}\times \mathscr{H}\to \mathbb{C}$ satisfying

1. $B(u,av+bw)=aB(u,v)+bB(u,w)$ for all $u,v,w\in \mathscr{H}$ and $a,b\in \mathbb{C}$.
2. $B(av+bw,u)=\overline{a}B(v,u)+\overline{b}B(w,u)$ for all $u,v,w\in \mathscr{H}$ and $a,b\in \mathbb{C}$.
3. $|B(u,v)|\leq C\|u\|\|v\|$ for all $u,v\in \mathscr{H}$ and some constant $C>0$.

There exists a unique bounded linear operator $A\in \mathscr{B}(\mathscr{H})$ such that $B(u,v)=\langle Au,v\rangle$ for all $u,v\in \mathscr{H}$. The norm of $A$ is the smallest constant $C$ such that $|B(u,v)|\leq C\|u\|\|v\|$ for all $u,v\in \mathscr{H}$.

[Proof ignored here]

The adjoint of a bounded operator

Let $A\in \mathscr{B}(\mathscr{H})$. And bounded sesqilinear form $B: \mathscr{H}\times \mathscr{H}\to \mathbb{C}$ such that $B(u,v)=\langle u,Av\rangle$ for all $u,v\in \mathscr{H}$. Then there exists a unique bounded linear operator $A^*\in \mathscr{B}(\mathscr{H})$ such that $B(u,v)=\langle A^*u,v\rangle$ for all $u,v\in \mathscr{H}$.

[Proof ignored here]

And $\|A^*\|=\|A\|$.

Additional properties of bounded operators:

Let $A,B\in \mathscr{B}(\mathscr{H})$ and $a,b\in \mathbb{C}$. Then

1. $(aA+bB)^*=\overline{a}A^*+\overline{b}B^*$.
2. $(AB)^*=B^*A^*$.
3. $(A^*)^*=A$.
4. $\|A^*\|=\|A\|$.
5. $\|A^*A\|=\|A\|^2$.

Definition of self-adjoint operator

An operator $A\in \mathscr{B}(\mathscr{H})$ is self-adjoint if $A^*=A$.

Definition of normal operator

An operator $N\in \mathscr{B}(\mathscr{H})$ is normal if $NN^*=N^*N$.

Definition of unitary operator

An operator $U\in \mathscr{B}(\mathscr{H})$ is unitary if $U^*U=UU^*=I$.

where $I$ is the identity operator on $\mathscr{H}$.

Definition of orthogonal projection

An operator $P\in \mathscr{B}(\mathscr{H})$ is an orthogonal projection if $P^*=P$ and $P^2=P$.

Tensor product of (infinite-dimensional) Hilbert spaces

Definition of tensor product

Let $\mathscr{H}_1$ and $\mathscr{H}_2$ be two Hilbert spaces. $u_1\in \mathscr{H}_1$ and $u_2\in \mathscr{H}_2$. Then $u_1\otimes u_2$ is an conjugate bilinear functional on $\mathscr{H}_1\times \mathscr{H}_2$.

Let $\mathscr{V}$ be the set of all finite lienar combination of such conjugate bilinear functionals. We define the inner product on $\mathscr{V}$ by

The infinite-dimensional tensor product of $\mathscr{H}_1$ and $\mathscr{H}_2$ is the completion (extension of those bilinear functionals to make the set closed) of $\mathscr{V}$ with respect to the norm induced by the inner product.

Denoted by $\mathscr{H}_1\otimes \mathscr{H}_2$.

The orthonormal basis of $\mathscr{H}_1\otimes \mathscr{H}_2$ is $\{u_i\otimes v_j:i=1,2,\cdots,j=1,2,\cdots\}$. where $u_i$ is the orthonormal basis of $\mathscr{H}_1$ and $v_j$ is the orthonormal basis of $\mathscr{H}_2$.

Fock space

Definition of Fock space

Let $\mathscr{H}^{\otimes n}$ be the $n$-fold tensor product of $\mathscr{H}$.

Set $\mathscr{H}^{\otimes 0}=\mathbb{C}$.

The Fock space of $\mathscr{H}$ is the direct sum of all $\mathscr{H}^{\otimes n}$.

For example, if $\mathscr{H}=L^2(\mathbb{R},\lambda)$, then an element in $\mathscr{F}(\mathscr{H})$ is a sequence of functions $\psi=(\psi_0,\psi_1(x_1),\psi_2(x_1,x_2),\cdots)$ such that $|\psi_0|^2+\sum_{n=1}^\infty \int|\psi_n(x_1,\cdots,x_n)|^2dx_1\cdots dx_n<\infty$.