CSE559A Lecture 9

Continue on ML for computer vision

Backpropagation

Computation graphs

SGD update for each parameter

$e$ is the error function.

Using the chain rule

Suppose $k=1$, $e=l(f_1(x,w_1),y)$

Example: $e=(f_1(x,w_1)-y)^2$

So $h_1=f_1(x,w_1)=w^\top_1x$, $e=l(h_1,y)=(y-h_1)^2$

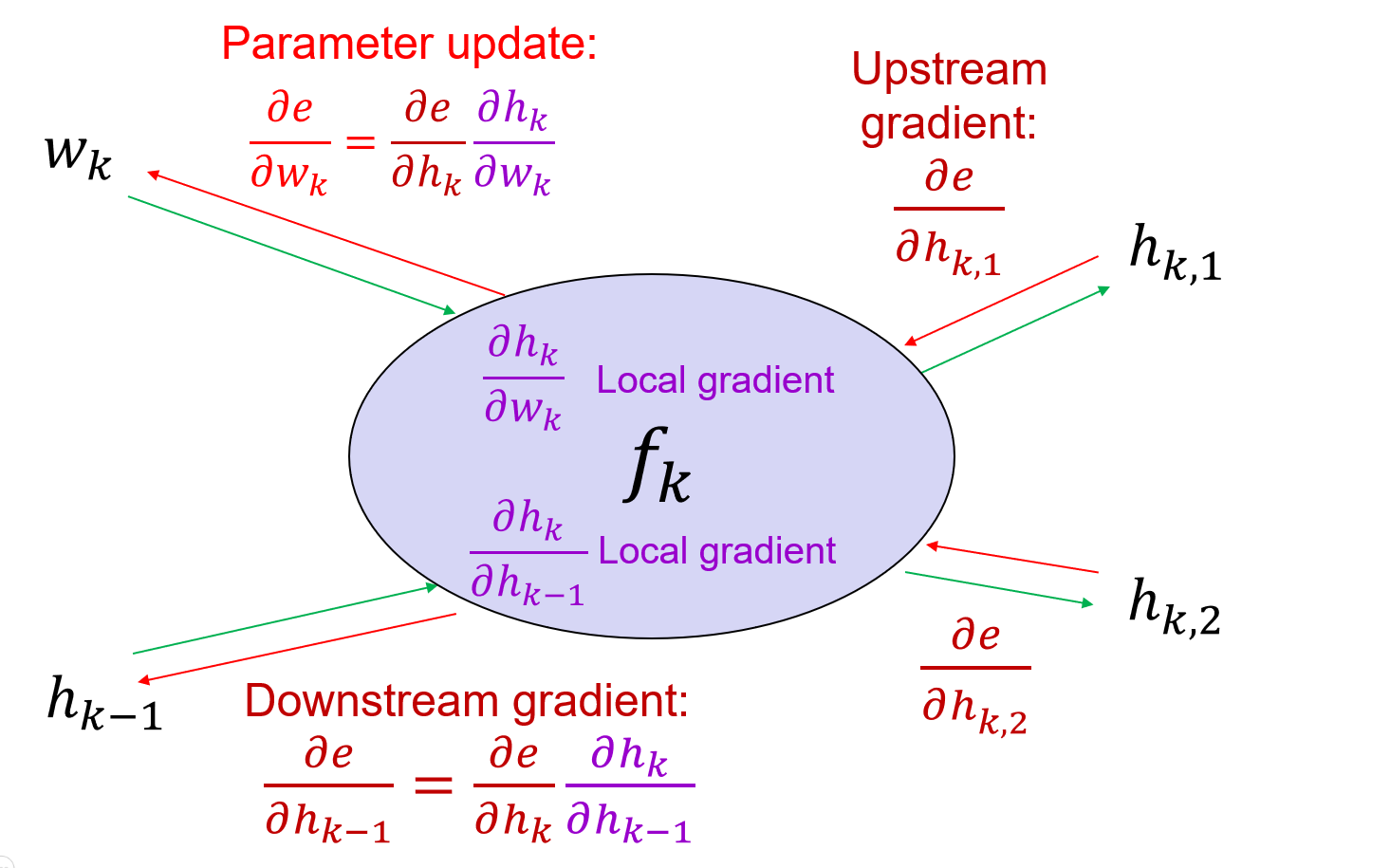
For the general cases,

Where the upstream gradient $\frac{\partial e}{\partial h_K}$ is known, and the local gradient $\frac{\partial h_k}{\partial w_k}$ is known.

General backpropagation algorithm

The adding layer is the gradient distributor layer. The multiplying layer is the gradient switcher layer. The max operation is the gradient router layer.

Simple example: Element-wise operation (ReLU)

$f(x)=ReLU(x)=max(0,x)$

Where $\frac{\partial z_i}{\partial x_j}=1$ if $i=j$ and $z_i>0$, otherwise $\frac{\partial z_i}{\partial x_j}=0$.

When $\forall x_i<0$ then $\frac{\partial z}{\partial x}=0$ (dead ReLU)

Other examples on ppt.

Convolutional Neural Networks

Basic Convolutional layer

Flatten layer

Fully connected layer, operate on vectorized image.

With the multi-layer perceptron, the neural network trying to fit the templates.

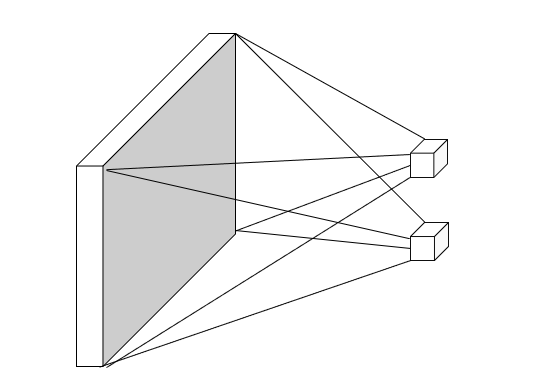
Convolutional layer

Limit the receptive fields of units, tiles them over the input image, and share the weights.

Equivalent to sliding the learned filter over the image , computing dot products at each location.

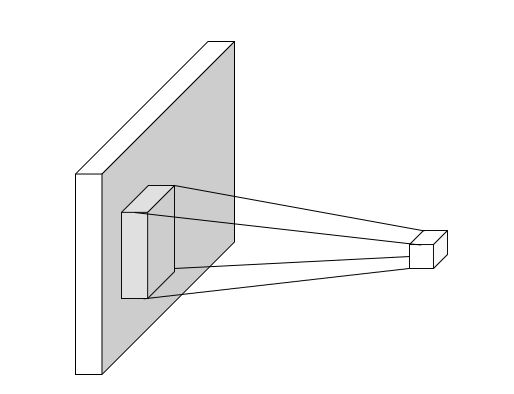
Padding: Add a border of zeros around the image. (higher padding, larger output size)

Stride: The step size of the filter. (higher stride, smaller output size)

Variants 1x1 convolutions, depthwise convolutions

Backward pass