CSE559A Lecture 26

Continue on Geometry and Multiple Views

The Essential and Fundamental Matrices

Math of the epipolar constraint: Calibrated case

Recall Epipolar Geometry

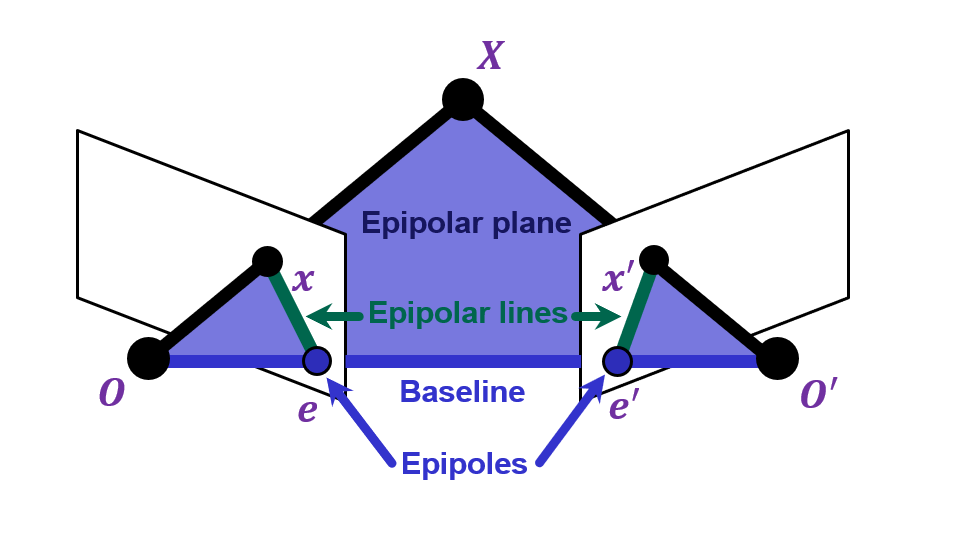
Epipolar Geometry Configuration

Epipolar constraint:

If we set the config for the first camera as the world origin and $[I|0]\begin{pmatrix}y\\1\end{pmatrix}=x$ , and $[R|t]\begin{pmatrix}y\\1\end{pmatrix}=x'$ , then

Notice that $x'\cdot [t\times (Ry)]=0$

x'^\top E x_1 = 0

We denote the constraint defined by the Essential Matrix as $E$ .

$E x$ is the epipolar line associated with $x$ ( $l'=Ex$ )

$E^\top x'$ is the epipolar line associated with $x'$ ( $l=E^\top x'$ )

$E e=0$ and $E^\top e'=0$ ( $x$ and $x'$ don’t matter)

$E$ is singular (rank 2) and have five degrees of freedom.

Epipolar constraint: Uncalibrated case

If the calibration matrices $K$ and $K'$ are unknown, we can write the epipolar constraint in terms of unknown normalized coordinates:

x'^\top_{norm} E x_{norm} = 0

where $x_{norm}=K^{-1} x$ , $x'_{norm}=K'^{-1} x'$

x'^\top_{norm} E x_{norm} = 0\implies x'^\top_{norm} Fx=0

where $F=K'^{-1}EK^{-1}$ is the Fundamental Matrix.

(x',y',1)\begin{bmatrix} f_{11} & f_{12} & f_{13} \\ f_{21} & f_{22} & f_{23} \\ f_{31} & f_{32} & f_{33} \end{bmatrix}\begin{pmatrix} x\\y\\1 \end{pmatrix}=0

Properties of $F$ :

$F x$ is the epipolar line associated with $x$ ( $l'=F x$ )

$F^\top x'$ is the epipolar line associated with $x'$ ( $l=F^\top x'$ )

$F e=0$ and $F^\top e'=0$

$F$ is singular (rank two) and has seven degrees of freedom

Estimating the fundamental matrix

Given: correspondences $x=(x,y,1)^\top$ and $x'=(x',y',1)^\top$

Constraint: $x'^\top F x=0$

(x',y',1)\begin{bmatrix} f_{11} & f_{12} & f_{13} \\ f_{21} & f_{22} & f_{23} \\ f_{31} & f_{32} & f_{33} \end{bmatrix}\begin{pmatrix} x\\y\\1 \end{pmatrix}=0

Each pair of correspondences gives one equation (one constraint)

At least 8 pairs of correspondences are needed to solve for the 9 elements of $F$ (The eight point algorithm)

We know $F$ needs to be singular/rank 2. How do we force it to be singular?

Solution: take SVD of the initial estimate and throw out the smallest singular value

F=U\begin{bmatrix} \sigma_1 & 0 \\ 0 & \sigma_2 \\ 0 & 0 \end{bmatrix}V^\top

Structure from Motion

Not always uniquely solvable.

If we scale the entire scene by some factor $k$ and, at the same time, scale the camera matrices by the factor of $1/k$ , the projections of the scene points remain exactly the same: $x\cong PX =(1/k P)(kX)$

Without a reference measurement, it is impossible to recover the absolute scale of the scene!

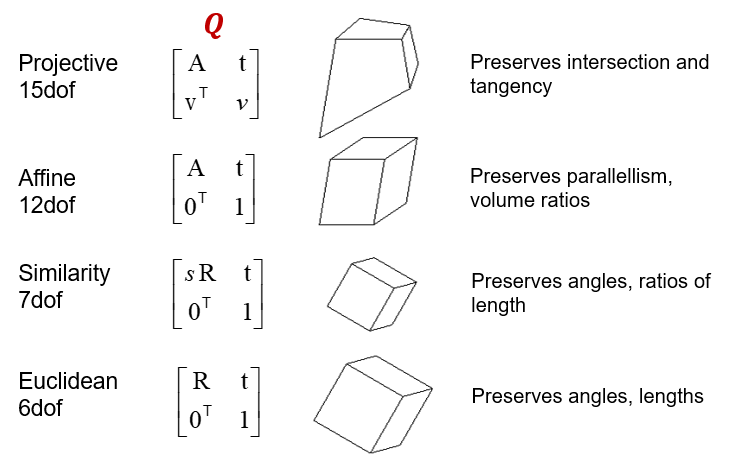
In general, if we transform the scene using a transformation $Q$ and apply the inverse transformation to the camera matrices, then the image observations do not change:

$x\cong PX =(P Q^{-1})(QX)$

Types of Ambiguities

Ambiguities in projection

Affine projection : more general than orthographic

A general affine projection is a 3D-to-2D linear mapping plus translation:

P=\begin{bmatrix} a_{11} & a_{12} & a_{13} & t_1 \\ a_{21} & a_{22} & a_{23} & t_2 \\ 0 & 0 & 0 & 1 \end{bmatrix}=\begin{bmatrix} A & t \\ 0^\top & 1 \end{bmatrix}

In non-homogeneous coordinates:

\begin{pmatrix} x\\y\\1 \end{pmatrix}=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix}\begin{pmatrix} X\\Y\\Z \end{pmatrix}+\begin{pmatrix} t_1\\t_2 \end{pmatrix}=AX+t

Affine Structure from Motion

Given: 𝑚 images of 𝑛 fixed 3D points such that

x_{ij}=A_iX_j+t_i, \quad i=1,\dots,m, \quad j=1,\dots,n

Problem: use the 𝑚𝑛 correspondences $x_{ij}$ to estimate 𝑚 projection matrices $A_i$ and translation vectors $t_i$ , and 𝑛 points $X_j$

The reconstruction is defined up to an arbitrary affine transformation $Q$ (12 degrees of freedom):

\begin{bmatrix} A & t \\ 0^\top & 1 \end{bmatrix}\rightarrow\begin{bmatrix} A & t \\ 0^\top & 1 \end{bmatrix}Q^{-1}, \quad \begin{pmatrix}X_j\\1\end{pmatrix}\rightarrow Q\begin{pmatrix}X_j\\1\end{pmatrix}

How many constraints and unknowns for $m$ images and $n$ points?

$2mn$ constraints and $8m + 3n$ unknowns

To be able to solve this problem, we must have $2mn \geq 8m+3n-12$ (affine ambiguity takes away 12 dof)

E.g., for two views, we need four point correspondences