CSE559A Lecture 22

Continue on Robust Fitting of parametric models

RANSAC

Definition: RANdom SAmple Consensus

RANSAC is a method to fit a model to a set of data points.

It is a non-deterministic algorithm that can be used to fit a model to a set of data points.

Pros:

Simple and general
Applicable to many different problems
Often works well in practice

Cons:

Lots of parameters to set
Number of iterations grows exponentially as outlier ratio increases
Can’t always get a good initialization of the model based on the minimum number of samples.

Hough Transform

Use point-line duality to find lines.

In practice, we don’t use (m,b) parameterization.

Instead, we use polar parameterization:

\rho = x \cos \theta + y \sin \theta

Algorithm outline:

Initialize accumulator $H$ $H$ to all zeros
- For each feature point $(x,y)$ $(x, y)$
  - For $\theta = 0$ to $180$
  - $\rho = x \cos \theta + y \sin \theta$
  - $H(\theta, \rho) += 1$
Find the value(s) of $(\theta, \rho)$ $(θ, ρ)$ where $H(\theta, \rho)$ $H (θ, ρ)$ is a local maximum (perform NMS on the accumulator array)
- The detected line in the image is given by $\rho = x \cos \theta + y \sin \theta$

Effect of noise

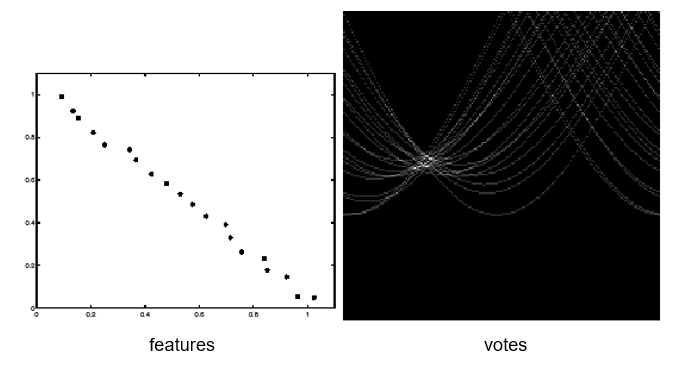
Hough transform with noise

Noise makes the peak fuzzy.

Effect of outliers

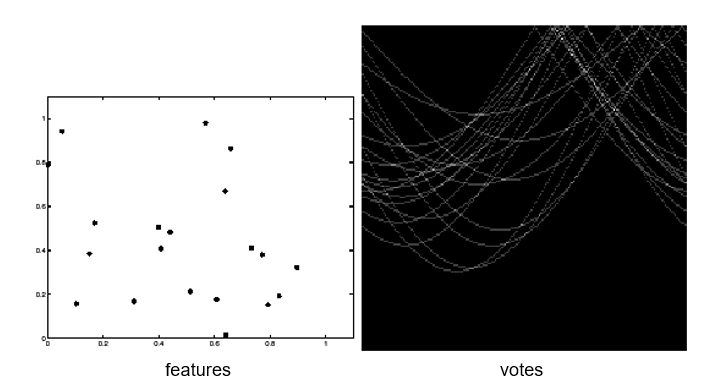
Hough transform with outliers

Outliers can break the peak.

Pros and Cons

Pros:

Can deal with non-locality and occlusion
Can detect multiple instances of a model
Some robustness to noise: noise points unlikely to contribute consistently to any single bin
Leads to a surprisingly general strategy for shape localization (more on this next)

Cons:

Complexity increases exponentially with the number of model parameters
- In practice, not used beyond three or four dimensions
Non-target shapes can produce spurious peaks in parameter space
It’s hard to pick a good grid size

Generalize Hough Transform

Template representation: for each type of landmark point, store all possible displacement vectors towards the center

Detecting the template:

For each feature in a new image, look up that feature type in the model and vote for the possible center locations associated with that type in the model

Implicit shape models

Training:

Build codebook of patches around extracted interest points using clustering
Map the patch around each interest point to closest codebook entry
For each codebook entry, store all positions it was found, relative to object center

Testing:

Given test image, extract patches, match to codebook entry
Cast votes for possible positions of object center
Search for maxima in voting space
Extract weighted segmentation mask based on stored masks for the codebook occurrences

Image alignment

Affine transformation

Simple fitting procedure: linear least squares Approximates viewpoint changes for roughly planar objects and roughly orthographic cameras Can be used to initialize fitting for more complex models

Fitting an affine transformation:

\begin{bmatrix} &&&\cdots\\ x_i & y_i & 0&0&1&0\\ 0&0&x_i&y_i&0&1\\ &&&\cdots\\ \end{bmatrix} \begin{bmatrix} m_1\\ m_2\\ m_3\\ m_4\\ t_1\\ t_2\\ \end{bmatrix} = \begin{bmatrix} \cdots\\ \end{bmatrix}

Only need 3 points to solve for 6 parameters.

Homography

Recall that

x' = \frac{a x + b y + c}{g x + h y + i}, \quad y' = \frac{d x + e y + f}{g x + h y + i}

Use 2D homogeneous coordinates:

$(x,y) \rightarrow \begin{pmatrix}x \\ y \\ 1\end{pmatrix}$

$\begin{pmatrix}x\\y\\w\end{pmatrix} \rightarrow (x/w,y/w)$

Reminder: all homogeneous coordinate vectors that are (non-zero) scalar multiples of each other represent the same point

Equation for homography in homogeneous coordinates:

\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} \cong \begin{pmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}

Constraint from a match $(x_i,x_i')$ , $x_i'\cong Hx_i$

How can we get rid of the scale ambiguity?

Cross product trick: $x_i' × Hx_i=0$

The cross product is defined as:

\begin{pmatrix}a\\b\\c\end{pmatrix} \times \begin{pmatrix}a'\\b'\\c'\end{pmatrix} = \begin{pmatrix}bc'-b'c\\ca'-c'a\\ab'-a'b\end{pmatrix}

Let $h_1^\top, h_2^\top, h_3^\top$ be the rows of $H$ . Then

x_i' × Hx_i=\begin{pmatrix} x_i' \\ y_i' \\ 1 \end{pmatrix} \times \begin{pmatrix} h_1^\top x_i \\ h_2^\top x_i \\ h_3^\top x_i \end{pmatrix} = \begin{pmatrix} y_i' h_3^\top x_i−h_2^\top x_i \\ h_1^\top x_i−x_i' h_3^\top x_i \\ x_i' h_2^\top x_i−y_i' h_1^\top x_i \end{pmatrix}

Constraint from a match $(x_i,x_i')$ :

x_i' × Hx_i=\begin{pmatrix} x_i' \\ y_i' \\ 1 \end{pmatrix} \times \begin{pmatrix} h_1^\top x_i \\ h_2^\top x_i \\ h_3^\top x_i \end{pmatrix} = \begin{pmatrix} y_i' h_3^\top x_i−h_2^\top x_i \\ h_1^\top x_i−x_i' h_3^\top x_i \\ x_i' h_2^\top x_i−y_i' h_1^\top x_i \end{pmatrix}

Rearranging the terms:

\begin{bmatrix} 0^\top &-x_i^\top &y_i' x_i^\top \\ x_i^\top &0^\top &-x_i' x_i^\top \\ y_i' x_i^\top &x_i' x_i^\top &0^\top \end{bmatrix} \begin{bmatrix} h_1 \\ h_2 \\ h_3 \end{bmatrix} = 0

These equations aren’t independent! So, we only need two.

Robust alignment

Descriptor-based feature matching

Extract features Compute putative matches Loop:

Hypothesize transformation $T$
Verify transformation (search for other matches consistent with $T$ )

RANSAC

Even after filtering out ambiguous matches, the set of putative matches still contains a very high percentage of outliers

RANSAC loop:

Randomly select a seed group of matches
Compute transformation from seed group
Find inliers to this transformation
If the number of inliers is sufficiently large, re-compute least-squares estimate of transformation on all of the inliers

At the end, keep the transformation with the largest number of inliers