CSE559A Lecture 19

Feature Detection

Behavior of corner features with respect to Image Transformations

To be useful for image matching, “the same” corner features need to show up despite geometric and photometric transformations

We need to analyze how the corner response function and the corner locations change in response to various transformations

Affine intensity change

Solution:

• Only derivative of intensity are used (invariant to intensity change)
• Intensity scaling

Image translation

Solution:

• Derivatives and window function are shift invariant

Image rotation

Second moment ellipse rotates but its shape (i.e. eigenvalues) remains the same

Scaling

Classify edges instead of corners

Automatic Scale selection for interest point detection

Scale space

We want to extract keypoints with characteristic scales that are equivariant (or covariant) with respect to scaling of the image

Approach: compute a scale-invariant response function over neighborhoods centered at each location $(x,y)$ and a range of scales $\sigma$, find scale-space locations $(x,y,\sigma)$ where this function reaches a local maximum

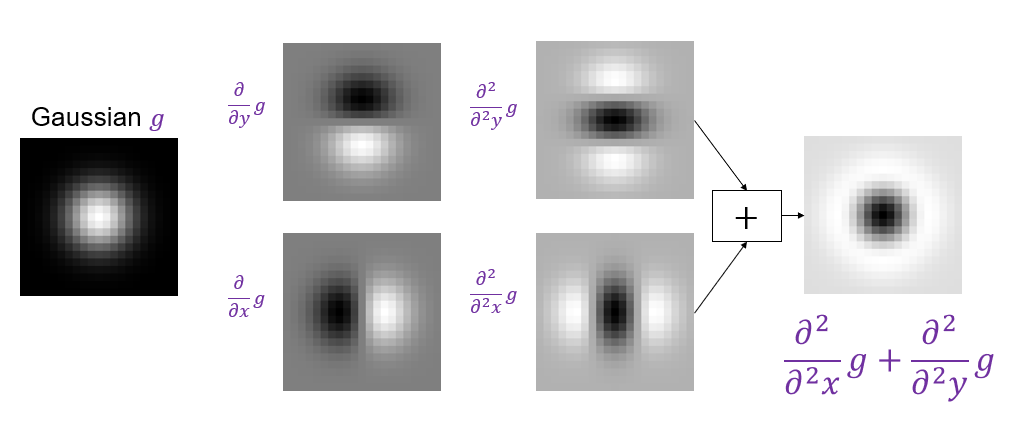
A particularly convenient response function is given by the scale-normalized Laplacian of Gaussian (LoG) filter:

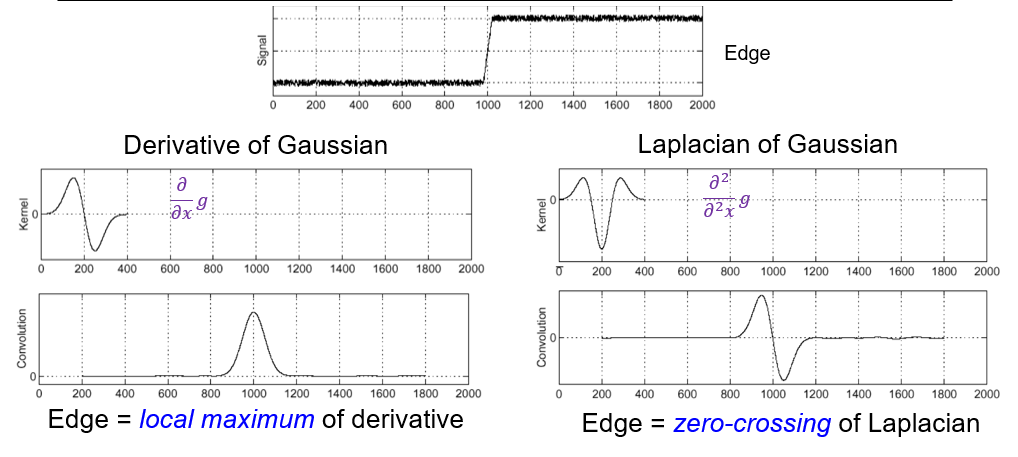
Edge detection with LoG

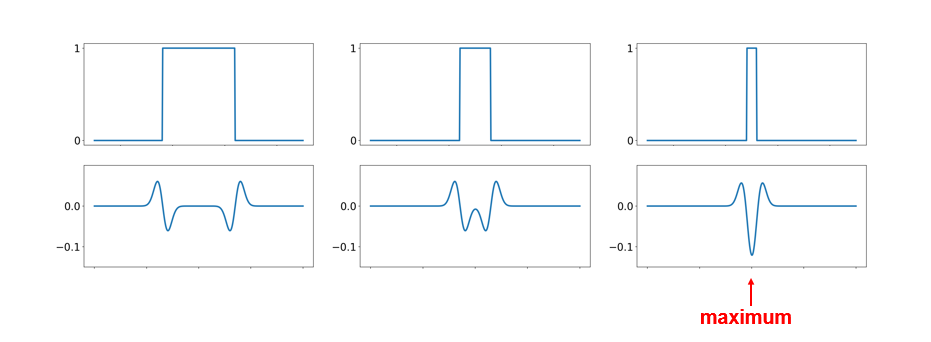
Blob detection with LoG

Difference of Gaussians (DoG)

DoG has a little more flexibility, since you can select the scales of the Gaussians.

Scale-invariant feature transform (SIFT)

The main goal of SIFT is to enable image matching in the presence of significant transformations

• To recognize the same keypoint in multiple images, we need to match appearance descriptors or “signatures” in their neighborhoods
• Descriptors that are locally invariant w.r.t. scale and rotation can handle a wide range of global transformations

Maximum stable extremal regions (MSER)

Based on Watershed segmentation algorithm

Select regions that are stable over a large parameter range