CSE510 Deep Reinforcement Learning (Lecture 3)

Introduction and Definition of MDPs

Definition and Examples

Reinforcement Learning

A computational framework for behavior learning through reinforcement

RL is for an agent with the capacity to act
Each action influences the agent’s future observation
Success is measured by a scalar reward signal
Goal: find a policy that maximizes expected total rewards

Mathematical Model: Markov Decision Processes (MDP)

Markov Decision Processes (MDP)

A Finite MDP is defined by:

A finite set of states $s \in S$
A finite set of actions $a \in A$
A transition function $T(s, a, s')$
Probability that a from s leads to s’, i.e., $P(s'| s, a)$
Also called the model or the dynamics
A reward function $R(s)$ ( Sometimes $R(s,a)$ or $R(s, a, s')$ )
A start state
A start state
Maybe a terminal state

A model for sequential decisionmaking problem under uncertaint

States

Stat is a snapshot of everything that matters for the next decision
Experience is a sequence of observations, actions, and rewards.
Observation is the raw input of the agent’s sensors
The state is a summary of the experience.

s_t=f(o_1, r_1, a_1, \ldots, a_{t-1}, o_t, r_t)

The state can include immediate “observations,” highly processed observations, and structures built up over time from sequences of observations, memories etc.
In a fully observed environment, $s_t= f(o_t)$

Action

Action = choice you make now
They are used by the agent to interact with the world.
They can have many different temporal granularities and abstractions.
Actions can be defined to be
- The instantaneous torques on the gripper
- The instantaneous gripper translation, rotation, opening
- Instantaneous forces applied to the objects
- Short sequences of the above

Rewards

Reward = score you get as a result
They are scalar values provided by the environment to the agent that indicate whether goals have been achieved,
- e.g., 1 if goal is achieved, 0 otherwise, or -1 for overtime step the goal is not achieved
Rewards specify what the agent needs to achieve, not how to achieve it.
The simplest and cheapest form of supervision, and surprisingly general.
Dense rewards are always preferred if available
- e.g., distance changes to a goal.

Dynamics or the Environment Model

Transition = dice roll the world makes after your choice.
How the state change given the current state and action

P(S_{t+1}=s'|S_t=s_t, A_t=a_t)

Modeling the uncertainty
- Everyone has their own “world model”, capturing the physical laws of the world.
- Human also have their own “social model”, by their values, beliefs, etc.
Two problems:
- Planning: the dynamics model is known
- Reinforcement learning: the dynamics model is unknown

Assumptions we have for MDP

First-Order Markovian dynamics (history independence)

Next state only depend on current state and current action

P(S_{t+1}=s'|S_t=s_t,A_t=a_t,S_1,A_1,\ldots,S_{t-1},A_{t-1}) = P(S_{t+1}=s'|S_t=s_t,A_t=a_t)

State-dependent reward

Reward is a deterministic function of current state

Stationary dynamics: do not depend on time

P(S_{t+1}=s'|A_t,S_t) = P(S_{k+1}=s'|A_k,S_k),\forall t,k

Full observability of the state

Though we can’t predict exactly which state we will reach when we execute an action, after the action is executed, we know the new state.

Examples

Atari games

States: raw RGB frames (one frame is not enough, so we use a sequence of frames, usually 4 frames)
Action: 18 actions in joystick movement
Reward: score changes

Go

States: features of the game board
Action: place a stone or resign
Reward: win +1, lose -1, draw 0

Autonomous car driving

States: speed, direction, lanes, traffic, weather, etc.
Action: steer, brake, throttle
Reward: +1 for reaching the destination, -1 for honking from surrounding cars, -100 for collision (exmaple)

Grid World

A maze-like problem

The agent lives in a grid
States: position of the agent
Noisy actions: east, south, west, north
Dynamics: actions not always go as planned
- 80% of the time, the action North takes the agent north (if there is a wall, it stays)
- 10% of the time, the action North takes the agent west and 10% of the time, the action North takes the agent east
Reward the agent receives each time step
- Small “living” reward each step (can be negative)
- Big reward for reaching the goal

Note

Due to the noise in the actions, it is insufficient to just output a sequence of actions to reach the goal.

Solution and its criterion

Solution to an MDP

Actions have stochastic effects, so the state we end up in is uncertain
This means that we might end up in states where the remainder of the action sequence doesn’t apply or is a bad choice
A solution should tell us what the best action is for any possible situation/state that might arise

Policy as output to an MDP

A stationary policy is a mapping from states to actions

$\pi: S \to A$
$\pi(s)$ is the action to take in state $s$ (regardless of the time step)
Specifies a continuously reactive controller

We don’t want to output just any policy

We want to output a good policy

One that accumulates a lot of rewards

Value of a policy

Value function

$V:S\to \mathbb{R}$ associates value with each state

\begin{aligned} V^\pi(s) &= \mathbb{E}\left[\sum_{t=0}^\infty \gamma^t R(s_t)|s_0=s,a_t=\pi(s_t), s_{t+1}|s_t,a_t\sim P\right] \\ &= \mathbb{E}\left[R(s_t) + \gamma \sum_{t=1}^\infty \gamma^{t-1} R(s_{t+1})|s_0=s,a_t=\pi(s_t), s_{t+1}|s_t,a_t\sim P\right] \\ &= R(s) + \gamma \sum_{s'\in S} P(s'|s,\pi(s)) V^\pi(s') \end{aligned}

Future rewards “discounted” by $\gamma$ per time step

We value the state by the expected total rewards from this state onwards, discounted by $\gamma$ for each time step.

A small $\gamma$ means model would short-sighted and reduce computation complexity.

Bellman Equation

Basically, it gives one step lookahead value of a policy.

V^\pi(s) = R(s) + \gamma \sum_{s'\in S} P(s'|s,\pi(s)) V^\pi(s')

Today’s value = Today’s reward + discounted future value

Optimal Policy and Bellman Optimality Equation

The goal for a MDP is to compute or learn an optimal policy.

An optimal policy is one that achieves the highest value at any state

\pi^* = \arg\max_\pi V^\pi(s)

We define the optimal value function suing Bellman Optimality Equation (Proof left as an exercise)

V^*(s) = R(s) + \gamma \max_{a\in A} \sum_{s'\in S} P(s'|s,a) V^*(s')

The optimal policy is

\pi^*(s) = \arg\max_{a\in A} \sum_{s'\in S} P(s'|s,a) V^*(s')

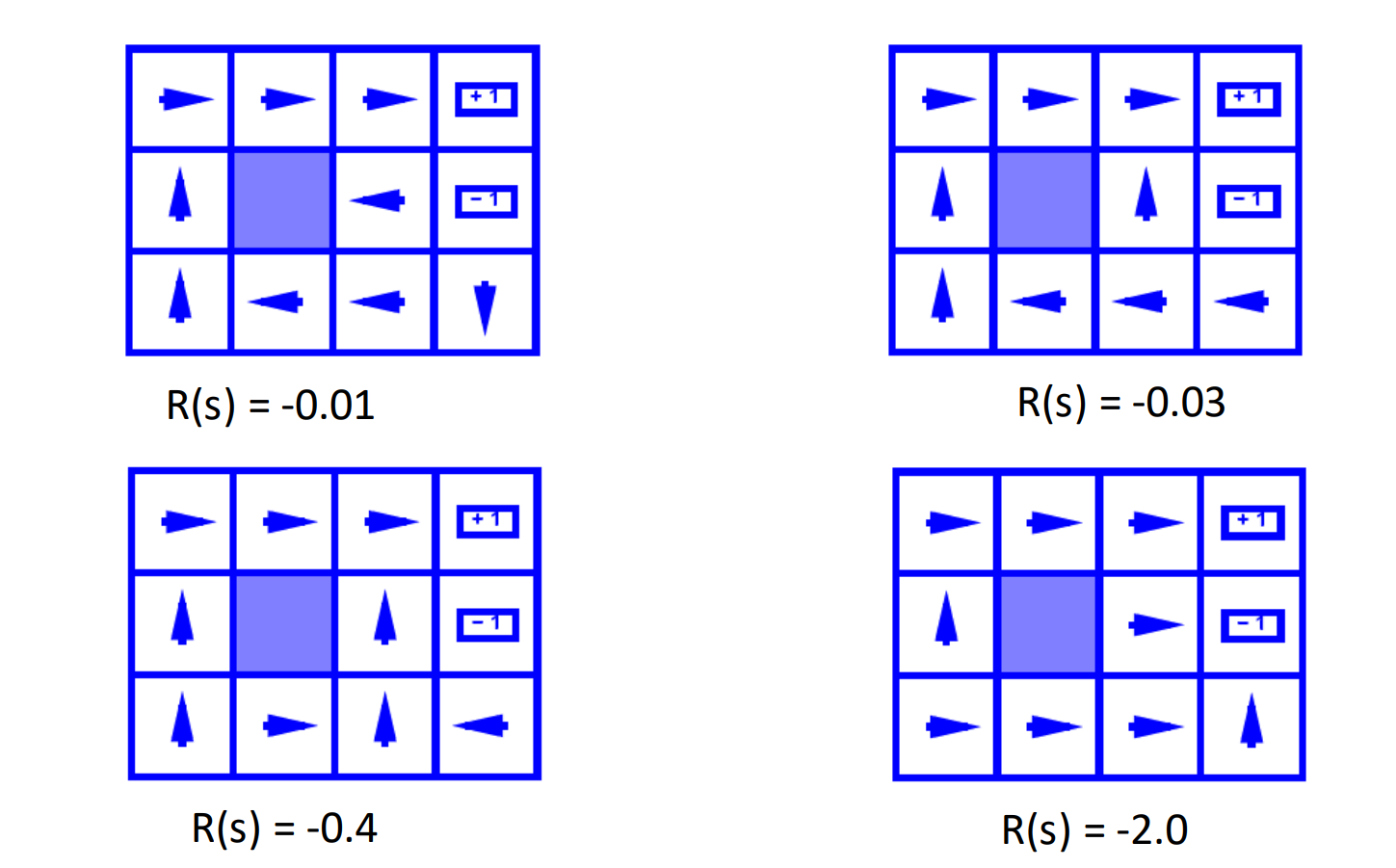
Optimal Policy